Intraocular Lens Power Calculation Using IOLMaster and Various Formulas in Short Eyes
Article information
Abstract
Purpose
To evaluate the predictability of intraocular lens (IOL) power calculations using the IOLMaster and four different IOL power calculation formulas (Haigis, Hoffer Q, SRK II, and SRK/T) for cataract surgery in eyes with a short axial length (AL).
Methods
The present study was a retrospective comparative analysis which included 25 eyes with an AL shorter than 22.0 mm that underwent uneventful phacoemulsification with IOL implantation from July 2007 to December 2008 at Seoul National University Boramae Hospital. Preoperative AL and keratometric power were measured by the IOLMaster, and power of the implanted IOL was determined using Haigis, Hoffer Q, SRK II, and SRK/T formulas. Postoperative refractive errors two months after surgery were measured using automatic refracto-keratometry (Nidek) and were compared with the predicted postoperative power. The mean absolute error (MAE) was defined as the average of the absolute value of the difference between actual and predicted spherical equivalences of postoperative refractive error.
Results
The MAE was smallest with the Haigis formula (0.37 ± 0.26 diopter [D]), followed by those of SRK/T (0.53 ± 0.25 D), SRK II (0.56 ± 0.20 D), and Hoffer Q (0.62 ± 0.16 D) in 25 eyes with an AL shorter than 22.0 mm. The proportion with an absolute error (AE) of less than 1 D was greatest in the Haigis formula (96%), followed by those in the SRK II (88%), SRK-T (84%), and Hoffer Q (80%).
Conclusions
The MAE was less than 0.7 D and the proportion of AE less than 1 D was more than 80% in all formulas. The IOL power calculation using the Haigis formula showed the best results for postoperative power prediction in short eyes.
Accuracy of intraocular lens (IOL) power calculation in cataract surgery is a very important factor associated with postoperative patient satisfaction [1-3]. With the recent development of multifocal IOL and an accommodative IOL, the accuracy of refractive errors after cataract surgery has been emphasized [4].
IOL power is predicted preoperatively using several different formulas and parameters. Measuring errors in these parameters and in the formulas constitute the sources of refractive error [5]. Imprecision in measurement of anterior chamber depth (ACD), axial length (AL), and corneal power contribute to 42%, 36% and 22% of errors, respectively [5]. The measurement of AL with partial coherence interferometry (IOLMaster; Carl Zeiss Meditech Inc., Dublin, CA, USA) has been shown to produce significantly more precise IOL power calculation and refractive outcome in cataract surgery, thereby avoiding possible compression of the eye with applanation A-scan ultrasound and difficulty with immersion A-scan ultrasound in AL measurements [6,7]. The source of error for postoperative refractive state prediction is due in part to the chosen formula, particularly in eyes with very long or very short AL [8,9].
The Haigis formula incorporated in the IOLMaster predicts effective lens position with improved ACD prediction algorithms and has shown more accurate IOL power prediction results, even in extreme eyes [8-10]. However, few reports have compared the accuracies of the various IOL power formulas for cataract surgery using partial coherence interferometry for eyes of short AL less than 22.0 mm.
The purpose of the present study was to evaluate the predictability of IOL power calculations using the IOLMaster and four different IOL power calculation formulas (Haigis, Hoffer Q, SRK II, and SRK/T) for cataract surgery in eyes with a short AL less than 22.0 mm.
Materials and Methods
The present study was a retrospective comparative analysis which included 25 eyes from 17 patients with an AL shorter than 22.0 mm and that underwent uneventful phacoemulsification with IOL implantation from July 2007 to December 2008. Preoperative AL, keratometric power, and ACD were measured by the IOLMaster version 3.01.0294. The power of the implanted IOL was determined using Haigis, Hoffer Q, SRK II, and SRK/T formulas calculated by the IOLMaster software. Postoperative refractive errors two months after cataract surgery were measured using automatic refracto-keratometry (RKT-7700; Nidek, Hiroishi, Japan) and were compared with the predicted postoperative power. The mean absolute error (MAE) was defined as the average of the absolute value of the differences between the actual and predicted spherical equivalences (SE) of the postoperative refractive error.
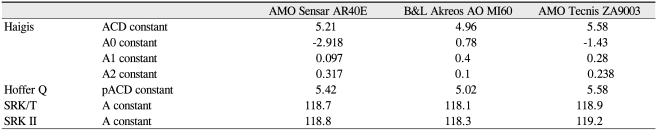
Cataract surgery was performed by two surgeons (YKH and SML). Topical anesthesia with proparacaine hydrochloride (Alcaine; Alcon Labs, Fort Worth, TX, USA) or subtenon anesthesia with 3% lidocaine was administered prior to the operation. A clear corneal incision 2.75 mm in width was made using a microkeratome at the superior or temporal cornea according to the axis of astigmatism, and phacoemulsification was performed after continuous curvilinear capsulorhexis. Three types of IOLs were used in the present study, Sensar® (AR40e; Abbott Medical Optics, Los Angeles, CA, USA; five eyes in three patients), Akreos-AO® (MI60; Bausch & Lomb, Rochester, NY, USA; ten eyes in seven patients), and Tecnis® (ZA9003, Abbott Medical Optics; ten eyes in seven patients); IOL was selected based only on the operation date and was not influenced by any other factors.
Cases were excluded if a posterior capsular rupture occurred during cataract surgery, if the IOL was inserted into the sulcus, or if the AL could not be measured using the IOLMaster. Also excluded from the present study were patients who could not be observed for at least two months after surgery.
The differences in the MAE according to the four IOL calculation formulas in the three IOL groups were analyzed. Furthermore, the proportions with absolute errors (AE) less than 0.5 diopters (D) and 1 D of the four IOL calculation formulas were estimated.
SPSS ver. 15.0 (SPSS Inc., Chicago, IL, USA) was used for statistical analysis. The Mann-Whitney U-test was used to compare differences in the AEs of the formulas. The ANOVA test was used for comparison of the AEs of the formulas according to the type of IOL. A statistically significant difference was defined as a p-value <0.05.
Results
A total of 25 eyes from 17 patients were included in the present study. One patient (one eye) was male and 16 patients (24 eyes) were female. The mean age was 70.6 ± 5.5 years (range, 61 to 80 years), and the mean follow-up period was 53.40 ± 15.71 months. The mean AL was 21.60 ± 0.41 mm (range, 20.41 to 21.94 mm). The ACD was 2.70 ± 0.36 mm (range, 2.07 to 3.34 mm).
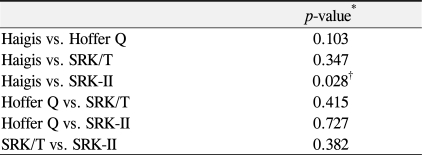
The constants applied in the four formulas of the IOLMaster in three IOL subtypes are shown in Table 1. The MAE was smallest in the Haigis formula (0.37 ± 0.26 D), followed by those of the SRK/T (0.53 ± 0.25 D), SRK II (0.56 ± 0.20 D), and Hoffer Q (0.62 ± 0.16 D) formulas (Fig. 1). The proportion of AE less than 0.5 D was greatest in the Haigis formula (76%), followed by those in the SRK II (60%), SRK-T (60%), and Hoffer Q (48%) formulas. Additionally, the proportion of AE less than 1 D was greatest in the Haigis formula (96%), followed by those in the SRK II (88%), SRK-T (84%), and Hoffer Q (80%) formulas (Fig. 2). No statistically significant discrepancies were observed in AE among the different IOL calculation formulas, except between the Haigis and the SRK-II formulas (p = 0.028, Mann-Whitney U-test) (Table 2).

Means and standard deviations of the absolute errors the four intraocular lens calculation formulas.
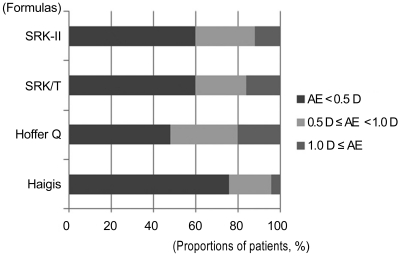
Proportion of the absolute errors (AE) less than 1 diopter (D) according to the intraocular lens formulas.
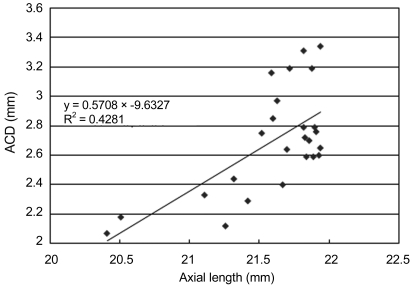
There were no statistically significant differences among the AEs of the three IOL groups according to ANOVA analysis (p-values, 0.116 for Haigis; 0.059 for Hoffer Q; 0.065 for SRK/T; 0.311 for SRK-II). A positive correlation between the AL and the preoperative ACD (Fig. 3) was revealed, although the coefficient of determination was low (linear regression analysis, R2 = 0.428).
Discussion
The IOLMaster used in the present study is adapted to a non-contact method known as partial coherence interferometry. This method has a higher resolution [11,12] and more reproducible measurements [13] compared with those of standard ultrasound transducers. However, the IOLMaster has several shortcomings, particularly in cases of mature or hypermature cataract, severe posterior capsular opacity, or a posterior segment abnormality, such as vitreous hemorrhage, because the AL is impossible to measure [5].
In the Haigis formula, the MAE was smallest and the proportion of AE less than 0.5 D or 1 D was greatest in the present study. Though the Haigis formula showed the best predictability, the SRK II, SRK/T, and Hoffer Q formulas also showed good prediction accuracies.
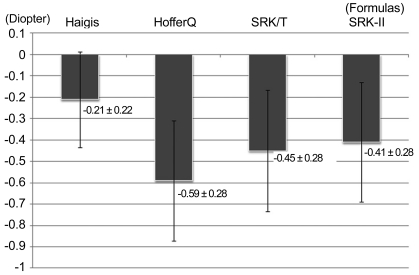
MAE is often used as an indicator for the IOL formula prediction accuracy; however, the MAE did not show a resulting direction (myopic or hyperopic). For the exact interpretation of the MAE result, predicted error (PE), which was back-calculated by subtracting the predicted SE from the postoperative SE, may be helpful where negative PE values indicate the tendency for myopic shifts, and vice versa. In the present study, PE showed several myopic shifts and was smallest in the Haigis formula (-0.21 ± 0.22 D), followed by those of the SRK II (-0.41 ± 0.28 D), SRK/T (-0.45 ± 0.28 D), and Hoffer Q (-0.59 ± 0.28 D) formulas (Fig. 4). Only the Hoffer Q formula showed a significant difference in PE compared with that of the Haigis formula (p = 0.020, Mann-Whitney U-test). MAE and PE results consistently showed that the Haigis formula was the most accurate of the four formulas in eyes with an AL shorter than 22.0 mm.
In the previous reports using partial coherence interferometry, Haigis and Hoffer Q formulas have been shown to perform better than Holladay 1 and SRK/T formulas in extremely hyperopic eyes where IOL power was 30.0 D or more [10]. Additionally, the Hoffer Q has been found to be more accurate than the SRK-T formula when AL is less than 22.0 mm according to the IOLMaster without the Haigis formula [14]. For hyperopic refractive lens exchange (AL less than 22.0 mm), the Haigis formula showed the smallest MAE, followed by those of the Holladay 2, Hoffer Q, and the SRK/T formulas, although the difference was not statistically significant [15].
The results in the present study are very similar to those of previous reports because the Haigis formula showed the smallest deviation from the targeted power compared to those of the other formulas. The MAE of the Haigis formula was 0.37 ± 0.26 D and the PE was -0.21 ± 0.22 D. In a previous retrospective analysis of 76 eyes from 56 patients with short AL who underwent cataract surgery with IOLs ranging in power from 30 D to 35 D, the MAE of the Haigis formula was 0.91 ± 0.09 D [10]. In that study, the MAE of the Hoffer Q formula was 1.13 ± 0.09 D, and the difference between the MAE of the Haigis formula and the Hoffer Q formula was statistically significant using a paired t test in 71 eyes (p = 0.037) [10]. In another study of 19 hyperopic eyes whose ALs were 22.0 mm or less, the MAE of the Haigis formula was 0.21 ± 0.21 D [15]. The MAE with the Haigis formula was significantly lower than the MAEs with the Hoffer Q (0.32 ± 0.20 D) and Holladay 2 formulas (0.29 ± 0.20 D) (p < 0.05, ANOVA with Bonferroni correction) [15]. The results were similar to those in the present study and became the basis for the Haigis formula being considered the most precise among the various formulas in short eyes.
Fig. 3 shows the relationship between AL and preoperative ACD in the present study, illustrating a positive correlation; however, the coefficient of determination is low (linear regression analysis, R2 = 0.428), consistent with a previous report [16]. Therefore, fixed ACD models such as the Binkhorst I formula predicted ACDs that were too short in long eyes and too long in short eyes [17]. As a consequence, a myopic error would be produced in a short eye and a hyperopic error in a long eye [17]. However, the mathematical prediction of ACD is very difficult, as shown by the low linearity in the present study. This determination renders the direct measurement of the ACD and lens thickness as more helpful for the exact positioning of the postoperative effective lens.
Because a given measurement error is a much larger portion of the AL in a short eye, any measurement error in the AL of a short eye would have a larger effect on final refractive error and thereby is a potentially important factor in regard to error [16]. Compression of the eye is believed to be part of the cause of AL shortening error, and this result still occurs even with experienced operators, although to a lesser degree [16]. Due to previous widespread use of an applanation ultrasound method that measures the AL to be shorter than the optical biometry method, other formulas may be designed with consideration of this fact [10]. Therefore, the Haigis formula using partial coherence interferometry is more accurate in short eyes.
Only the SRK II formula showed significant difference in MAE compared with that of the Haigis formula (p = 0.028, Mann-Whitney U-test), while other comparisons of the MAE among the formulas did not show any statistically significant differences. These results indicate that the Haigis formula can more precisely predict the postoperative refractive errors compared to those of the SRK II formula in eyes with short ALs less than 22.0 mm. In a previous report, the short eyes whose ALs were 23.0 mm or less were associated with significantly greater hyperopic shifts in postoperative refraction as determined by the SRK-II formula but not with the SRK/T formula (p = 0.008) [18], similar to the results in the present study.
The MAE and PE of Hoffer Q were the largest among the four formulas in the present study, a result contrary to those of previous reports and the common belief the Hoffer Q is a relatively good IOL-predicting formula, especially in short eyes [10,14]. The authors of the present study could not determine the reason for the errors with the Hoffer Q formula. A possible explanation is the lack of individualization of IOL constants, a shortcoming of the present study, considering that the standard deviation of the PE of the Hoffer Q formula was no larger than those of the other formulas, except the Haigis formula.
The retrospective nature, a relatively small sample number, three different IOL types and IOL constants which did not consider surgeon factors were limitations in the present study. Nevertheless, the present study showed the results of IOL power prediction in short ALs using the IOLMaster and the Haigis formula as the most precise among the various IOL formulas, though there was only statistical difference in comparison with SRK II formulas. Additionally, the results showed that the MAE was less than 0.7 D, and the proportion of the AE less than 1.0 D was greater than 80% in all four formulas using the IOLMaster.
In conclusion, the IOL power calculation using the IOLMaster showed relatively good postoperative IOL power prediction in short eyes with the Haigis, the Hoffer Q, the SRK-T, and the SRK II formulas. The Haigis formula showed the best results for postoperative power prediction in short eyes in which AL was less than 22.0 mm.
Notes
This study was previously presented in part as a poster at The American Society of Cataract and Refractive Surgery, Symposium and Congress, San Francisco, California, USA, April 2009.
No potential conflict of interest relevant to this article was reported.