|
 |
| Korean J Ophthalmol > Volume 33(3); 2019 > Article |
Abstract
Purpose
To explore spatial and temporal characteristics of glaucomatous visual field (VF) progression through multi-way decomposition of data.
Methods
Six serial VF exams with intervals of 6.0 ± 1.0 months in 121 pre-perimetric glaucoma eyes and 80 perimetric glaucoma eyes were arranged into a three-dimensional cube. The data were decomposed using parallel factor analysis.
Results
Three tri-linear components (i.e., spatial scores, temporal loadings, and subject-specific loadings) were identified. Component 1 clearly showed differences between superior and inferior hemispheres, linear trends over time, and wide variability in perimetric glaucoma. Findings were compatible with well-known characteristics of glaucomatous VF defects. Component 2 showed nasal and central areas in contrast with superior, inferior, and temporal peripheral locations, whereas component 3 showed a contrast between nasal and temporal hemispheres. Both components 2 and 3 failed to show clear temporal trends.
Glaucoma is a disease characterized by loss of retinal ganglion cells and the retinal nerve fiber layer, which eventually leads to deterioration of visual function [1]. Functional deterioration is currently measured by standard automated perimetry. An accurate and reliable method is needed to measure deterioration of the visual field (VF) to monitor the progression of glaucoma and evaluate the efficacy of therapies. Predicting future VF changes is currently one of the most challenging areas in managing glaucoma. To predict VF accurately, identifying the temporal and spatial characteristics of VF changes is essential. In structural aspects, VF data can be interpreted as multi-dimensional data, containing multiple VF locations for each test performed in every single patient. Past research on VF has focused on contemporary cross-sectional analysis [1,2,3,4] on regression methods applied separately in different locations (pointwise approach) [5,6,7,8,9], or on regression analysis based on global indices [10,11,12].
Cross-sectional approaches cannot capture any temporal variability, (i.e., progression of VF defects) because the data is a collection of single tests on each subject. VF locations reflect specific locations in individual human retinas, and each location should be correlated with the others (possible correlations are 52 × 52 = 2,074 correlations) because of the anatomical patterns of retinal nerve fibers and ganglion cells [13,14,15]. Because models based on point-wise approaches separately analyze discrete VF locations, these models have inherent difficulty incorporating such correlations among the locations. Some recently developed regression models capture spatial characteristics by analyzing clusters rather than individual points, either following point-wise regression [13] or prior to regression [16,17]. Also notable is the application of a Monte-Carlo simulation in analysis of spatial correlations in retinal sensitivity changes [18]. Using pattern deviation plot values from a baseline to two follow-up tests, probabilities were calculated for negative changes in one of 52 VF locations (in a 24-2 pattern, excluding two blind-spot locations). The results were compared with Monte-Carlo simulation results, providing solid evidence of spatial correlations in VF defect patterns in a glaucoma population. Location-wise aggregate results cannot reflect any subject-specific characteristics, however, and the large number of parameters (2,704 probabilities for each given level of defect) makes it difficult to integrate this methodology into a practical diagnostic framework.
Hence, this study introduces a multi-dimensional approach implementing a multi-modal decomposition method known as parallel factor analysis/canonical polyadic decomposition (PARAFAC/CANDECOMP) to incorporate intra-subject, inter-subject, and temporal variability into a single framework for simultaneous characterization of temporal and spatial features of glaucomatous VF. Using this approach, we analyze the characteristics of longitudinal VF data in our cohort of glaucoma patients.
Medical records of glaucoma patients who were followed with a Humphrey VF analyzer (Carl Zeiss Meditec, Dublin, CA, USA) at the glaucoma clinic in the department of ophthalmology at Asan Medical Center between January 2007 and August 2013 were retrospectively reviewed. Eyes with more than six serial regular reliable VF exams (false-positive errors <15%, false-negative errors <15%, and fixation loss <20%) at intervals of 6.0 ± 1.0 months (150 to 210 days) were enrolled. Initial exams were eliminated from analysis to minimize learning effects. All participants had best-corrected visual acuity of 20 / 40 or better, with a spherical refractive error between −6.0 and +4.0 diopters (D) and a cylinder correction within +3 D. All participants had a normal anterior chamber and an open-angle on slit-lamp and gonioscopic examinations. A glaucomatous VF defect was defined as a cluster of three points with a probability <5% on the pattern deviation map in at least one hemifield, including at least one point with a probability of <1%, a cluster of two points with a probability of <1% and a glaucoma hemifield test result outside normal limits, or a pattern standard deviation outside 95% of normal limits at baseline. Participants who had both glaucomatous optic disc changes (cup to disc ratio ≥0.7, diffuse or focal neural rim thinning, disc hemorrhage, or retinal nerve fiber layer defects) and a glaucomatous VF defect were defined as the perimetric glaucoma group (PG). Patients who had glaucomatous optic disc changes but a normal VF at baseline were assigned to the pre-perimetric glaucoma group (PPG). Exclusion criteria included the presence of any neuro-ophthalmic disorders, retinal diseases, a history of intraocular surgery other than uncomplicated cataract and glaucoma surgery at baseline, and/or a history of any intraocular surgery during the follow-up period. All included patients had a baseline VF mean deviation no worse than −9.0 decibels to control heterogeneity among subjects.
This study adhered to the Declaration of Helsinki principles and the study protocol was approved by the institutional review board of the Asan Medical Center, University of Ulsan, Seoul, Korea (2017-1311). Informed consent was waived due to the retrospective nature of the study.
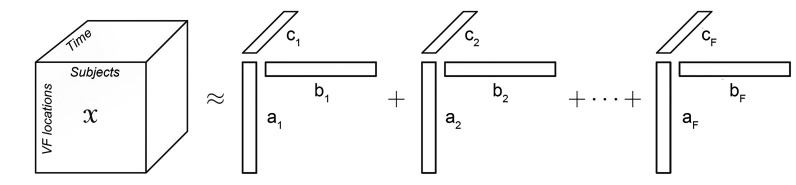
The PARAFAC/CANDECOMP method was introduced in 1970 [19,20] in psychometrics and has been widely adopted in chemometrics as well [21]. Recently, the method has gained some interest in space-time signal brain analysis, electroencephalography analysis [22,23] and functional neuroimaging [24,25]. The PARAFAC/CANDECOMP can be seen as a three-mode extension of principal component analysis and aims to reduce three-mode data table X by extracting the same number of components (F) for every mode [26]. Data table X is represented as the sum of each tri-linear component and residual E, usually presented as follows:
where aif, bjf, ckf are elements of the loading matrices A, B, and C, respectively. Term eijk represents elements of residual matrix E.
The equation can be additionally presented in matrix form after dropping residuals (eijk) as:
where af, bf, cf are the fth columns of the loading matrices A, B, and C, respectively.
An important advantage of PARAFAC/CANDECOMP in comparison to other techniques such as bilinear principal component analysis or independent component analysis is that the solution is unique without additional orthogonality or independence constraints as long as the right number of components is used and the signal-to-noise ratio is appropriate [21,23,27]. In previous research, PARAFAC/CANDECOMP analysis was calculated with R ver. 3.0.2, function CP of R statistical package ThreeWay ver. 1.1.1 (http://cran.r-project.org/web/packages/ThreeWay/) [28]. Other statistics were analyzed with SPSS ver. 15.0 (SPSS Inc., Chicago, IL, USA).
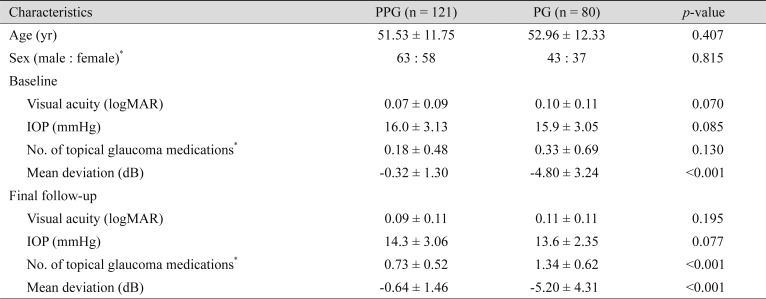
One hundred and twenty-one PPG and 80 PG eyes were included in the final analysis. The 121 PPG eyes were comprised of 63 male and 58 female eyes. In PG eyes, 43 and 37 were male and female eyes, respectively. Clinical characteristics of the participants assessed at baseline and at final follow-up examinations are described in Table 1. In PG subjects, measures of VF mean deviation were worse at both baseline and final visits, as expected (−0.32 ± 1.30 vs. −4.80 ± 3.24, p < 0.001). Visual acuity, intraocular pressure, and number of glaucoma medications showed no significant differences between the two groups.
A graphical representation of our model is shown in Fig. 1. The first mode represents specific locations on the VF map (spatial mode), and is labeled as “VF locations.” The second mode represents subjects (subject mode), and the third mode represents time (time mode). After centering raw data across the first and second modes, we ran PARAFAC/CANDECOMP analysis with one to six components (components 1 to 6) to determine the optimal number of components. The model's goodness-of-fit improved as the number of components increased, but a rapid decline in core consistency was shown with each additional components, especially after the fourth component (two components 100%, three components 90.16%, and four components 33.87%) [28]. Thus, a three-component-model with a fit of 51.76% (Fig. 2) was chosen for further analysis.
The VF map with corresponding spatial scores of each component is presented in Fig. 3A-3D. Because raw data were centered prior to analysis, scores can be interpreted as the deviation from the m ean. For every V F test, the signs and scales of spatial scores of each component were analyzed after modifying the corresponding subject and time mode loadings. Hence, the signs of scores in the component can be inversed, and comparison of magnitude of each scale should be done only within the component.
Component 1 clearly shows a contrast between superior and inferior hemispheres, suggesting that vertical hemispheric differences are the most prominent feature of glaucomatous VF defects in the study population. Scores are generally smaller in temporal areas, and larger along inferior and superior arcuate locations (superonasal SN01-04, SN10-13, superotemporal ST10-11; inferonasal IN10-13, IN20-22, and inferotemporal IT10-11, IT20). The spatial patterns of components 2 and 3 are less clear. In component 2, positive scores are mostly located in superior (superior rows 2, 3) and temporal (temporal columns 2, 3) peripheral areas, whereas nasal negative scores are mostly located in nasal (SN01-04, IN01-04, and IN11-13) and central areas (SN00 and ST00). Component 3 is slightly C-shaped, with a mainly horizontal contrast, having scores that are mostly nasally located except for two central (SM00 and IN00) negative signs, and the strongest positive scores in superior central locations (SN00 and ST00-01). Components 2 and 3 might represent other aspects of glaucomatous VF defects or might indicate normal variability.
The temporal loadings of component 1 increased with the passage of time, showing a clear linear pattern. Components 2 and 3 did not show the same trend (Fig. 4A-4C).
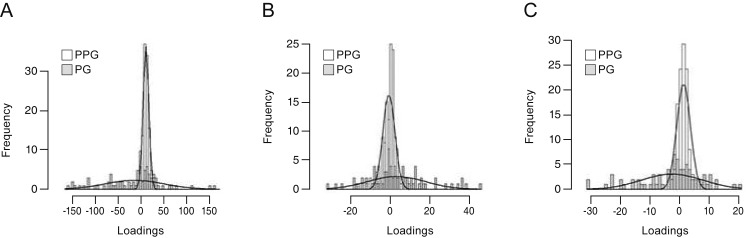
The mean loadings differed significantly between groups in all three components, with differences being most prominent in component 1 (Table 2). Distribution in PPG subjects was more concentrated near zero, whereas PG subjects had wider and subnormal distributions in all three components, with outstanding variance in component 1 (Fig. 5A-5C). To further assess structural differences in component loadings between the groups, we calculated the correlation between components within subjects. Within PPG subjects, component 2 had highly significant correlations with component 1 (0.296, p < 0.01) and component 3 (−0.516, p < 0.01). In contrast, components 1 and 3 had no significant correlation. No pair of components with a high correlation was detected in PG subjects (Table 3).
Various methodologies have been developed for analyzing multi-dimensional data in neuroscience and are being extended to fields of clinical diagnosis [29,30,31,32,33]. Applications in glaucoma have not been found in existing literature to date. Our PARAFAC/CANDECOMP analysis is a data-driven approach, drawing conclusions from the data itself rather than from pre-defined strict assumptions and models. Thus, this new approach enables simultaneous analysis of spatial, temporal and subject-specific characteristics, providing a more comprehensive and unbiased understanding of glaucomatous VF.
Turning to the data herein, component 1 had outstandingly high variability among three components, suggesting the importance of component 1 in explaining glaucomatous VF defects in the study population. On the spatial map, component 1 showed a clear vertical contrast, (i.e., differences between superior and inferior areas), which is a well-known feature of glaucomatous VF defects. In addition, component 1 showed a clear linear trend over time, suggesting increasing contrast between superior and inferior hemispheres in the study population over time. Such a clear temporal trend confers the possibility of developing a predictive scheme based on multi-mode data analysis, predicting not only the general rate of decline but also the patterns of progression.
The sharp contrast in distributions in component 1 loadings between PPG and PG shows the potential of multi-dimensional decomposition methodology for discerning glaucomatous VF defects from other types of VF defects. Patients with PPG in our study included those without apparent glaucomatous VF defects, but with clinical features of glaucomatous optic discs. Thus, it is not clear whether PPG results represent normal or early glaucomatous changes in retinal ganglion cells with non-significant VF defects [15]. Further prospective research including presumed normal controls and PPG patients might reveal novel characteristics of very early glaucomatous VF damage, thereby facilitating earlier diagnosis.
In PPG patients herein, component 2 is correlated with components 1 and 3. This relationship may be explained insofar as components 2 and 3 compensated for component 1 in patients with a pre-perimetric status. In PG patients, however, where the variability of loadings was much higher, the relationship becomes vague. There is a possibility that a different complementary set of components existed in the two groups. Further research with longer follow-up time and more components is necessary.
More detailed identification of glaucomatous VF patterns was not possible due to insufficient data and the limited number of components. With more data and sophisticated methodologies with more patterns, sub-patterns of glaucomatous VF defects might be identified along with pattern-specific progression rates.
Collecting large amounts of reliable VF data is difficult due to 1) the long timescale of VF progression, 2) limited follow-up time because of various clinical and personal factors, 3) variability in interval periods between subsequent tests, and 4) treatments and interventions affecting progression rates and patterns [34].
With the recent development of precise diagnostic modalities, intense research has emerged in assessing clinical implications of sophisticated measurements in the field of glaucoma—specifically in optical coherence tomography [35,36]. In this context, we expect that multi-dimensional approaches will find wider use. Current methodologies include only VF retinal sensitivity data, but multi-way decompositions can be extended to include more dimensions, namely demographic data (age, sex, and other characteristics), physical examination data (intraocular pressure, cataract and angle grading, and other physical features), and other diagnostic modalities, such as optical coherence tomography, by combining spatial and structural information.
We expect that the future development of more suitable models and collection of longer-term follow-up data will overcome many of the existing difficulties described.
Notes
Conflict of Interest: No potential conflict of interest relevant to this article was reported.
REFERENCES
1. Goldbaum MH. Unsupervised learning with independent component analysis can identify patterns of glaucomatous visual field defects. Trans Am Ophthalmol Soc 2005;103:270-280.



2. Asman P, Heijl A. Glaucoma hemifield test: automated visual field evaluation. Arch Ophthalmol 1992;110:812-819.


3. Marin-Franch I, Swanson WH, Malinovsky VE. A novel strategy for the estimation of the general height of the visual field in patients with glaucoma. Graefes Arch Clin Exp Ophthalmol 2014;252:801-809.



4. Iester M, De Feo F, Douglas GR. Visual field loss morphology in high- and normal-tension glaucoma. J Ophthalmol 2012;2012:327326.



5. Nouri-Mahdavi K, Hoffman D, Gaasterland D, Caprioli J. Prediction of visual field progression in glaucoma. Invest Ophthalmol Vis Sci 2004;45:4346-4351.


6. Wilkins MR, Fitzke FW, Khaw PT. Pointwise linear progression criteria and the detection of visual field change in a glaucoma trial. Eye (Lond) 2006;20:98-106.


7. De Moraes CG, Liebmann CA, Susanna R Jr, et al. Examination of the performance of different pointwise linear regression progression criteria to detect glaucomatous visual field change. Clin Exp Ophthalmol 2012;40:e190-e196.


8. Viswanathan AC, Fitzke FW, Hitchings RA. Early detection of visual field progression in glaucoma: a comparison of PROGRESSOR and STATPAC 2. Br J Ophthalmol 1997;81:1037-1042.



9. Caprioli J, Mock D, Bitrian E, et al. A method to measure and predict rates of regional visual field decay in glaucoma. Invest Ophthalmol Vis Sci 2011;52:4765-4773.


10. Bengtsson B, Heijl A. A visual field index for calculation of glaucoma rate of progression. Am J Ophthalmol 2008;145:343-353.


11. Cho JW, Sung KR, Yun SC, et al. Progression detection in different stages of glaucoma: mean deviation versus visual field index. Jpn J Ophthalmol 2012;56:128-133.


12. Bengtsson B, Patella VM, Heijl A. Prediction of glaucomatous visual field loss by extrapolation of linear trends. Arch Ophthalmol 2009;127:1610-1615.


13. Nouri-Mahdavi K, Mock D, Hosseini H, et al. Pointwise rates of visual field progression cluster according to retinal nerve fiber layer bundles. Invest Ophthalmol Vis Sci 2012;53:2390-2394.


14. Strouthidis NG, Vinciotti V, Tucker AJ, et al. Structure and function in glaucoma: the relationship between a functional visual field map and an anatomic retinal map. Invest Ophthalmol Vis Sci 2006;47:5356-5362.


15. Quigley HA, Dunkelberger GR, Green WR. Retinal ganglion cell atrophy correlated with automated perimetry in human eyes with glaucoma. Am J Ophthalmol 1989;107:453-464.


16. Yousefi S, Goldbaum MH, Balasubramanian M, et al. Learning from data: recognizing glaucomatous defect patterns and detecting progression from visual field measurements. IEEE Trans Biomed Eng 2014;61:2112-2124.



17. Bresson-Dumont H, Hatton J, Foucher J, Fonteneau M. Visual field progression in glaucoma: cluster analysis. J Fr Ophtalmol 2012;35:735-741.


18. Pascual JP, Schiefer U, Paetzold J, et al. Spatial characteristics of visual field progression determined by Monte Carlo simulation: diagnostic innovations in glaucoma study. Invest Ophthalmol Vis Sci 2007;48:1642-1650.


19. Carroll JD, Chang JJ. Analysis of individual differences in multidimensional scaling via an N-way generalization of “Eckart-Young” decomposition. Psychometrika 1970;35:283-319.

20. Harshman RA. Foundations of the PARAFAC procedure: models and conditions for an “explanatory” multimodal factor analysis. Los Angeles: University of California at Los Angeles; 1970. p. 1-84.
22. Deburchgraeve W, Cherian PJ, De Vos M, et al. Neonatal seizure localization using PARAFAC decomposition. Clin Neurophysiol 2009;120:1787-1796.


23. Miwakeichi F, Martinez-Montes E, Valdes-Sosa PA, et al. Decomposing EEG data into space-time-frequency components using Parallel Factor Analysis. Neuroimage 2004;22:1035-1045.


24. Beckmann CF, Smith SM. Tensorial extensions of independent component analysis for multisubject FMRI analysis. Neuroimage 2005;25:294-311.


25. Martinez-Montes E, Valdes-Sosa PA, Miwakeichi F, et al. Concurrent EEG/fMRI analysis by multiway Partial Least Squares. Neuroimage 2004;22:1023-1034.


26. Giordani P, Kiers HA, Del Ferraro MA. Three-way component analysis using the R package ThreeWay. J Stat Softw 2014;4 22
27. Kruskal JB. Three-way arrays: rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics. Linear Algebra Appl 1977;18:95-138.

28. Del Ferraro MA, Kiers HA, Giordani P. ThreeWay: three-way component analysis (version 1.1.3) [Internet]. [place unknown]: Comprehensive R Archive Network; 2015. cited 2018 Dec 18. Available: https://cran.r-project.org/web/packages/ThreeWay/.
29. He B, Liu Z. Multimodal functional neuroimaging: integrating functional MRI and EEG/MEG. IEEE Rev Biomed Eng 2008;1:23-40.



30. Varoquaux G, Sadaghiani S, Pinel P, et al. A group model for stable multi-subject ICA on fMRI datasets. Neuroimage 2010;51:288-299.


31. Robinson SD, Schopf V. ICA of f MRI studies: new approaches and cutting edge applications. Front Hum Neurosci 2013;7:724



32. Sui J, Pearlson G, Caprihan A, et al. Discriminating schizophrenia and bipolar disorder by fusing f MRI and DTI in a multimodal CCA+ joint ICA model. Neuroimage 2011;57:839-855.



33. Weis M, Jannek D, Roemer F, et al. Multi-dimensional PARAFAC2 component analysis of multi-channel EEG data including temporal tracking. Conf Proc IEEE Eng Med Biol Soc 2010;2010:5375-5378.

34. De Moraes CG, Demirel S, Gardiner SK, et al. Effect of treatment on the rate of visual field change in the ocular hypertension treatment study observation group. Invest Ophthalmol Vis Sci 2012;53:1704-1709.



Fig. 2
Goodness of fit (%) with varying number of components (the number under each point denotes the number of components included in the analysis).
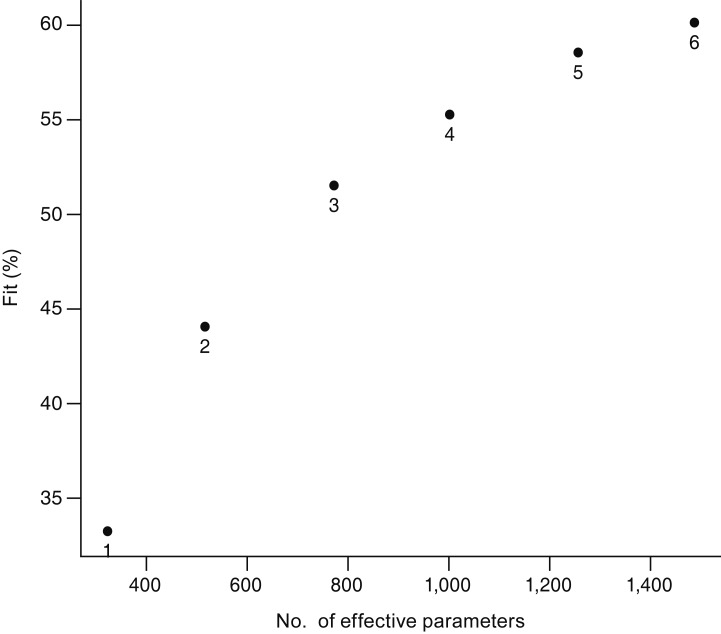
Fig. 3
Spatial scores of three components. (A) Component 1, (B) component 2, and (C) component 3 are arranged to match visual field locations (both eyes presented as the right eye). (D) Reference map of visual field locations. SN = superonasal; ST = superotemporal; IN = inferonasal; IT = inferotemporal.
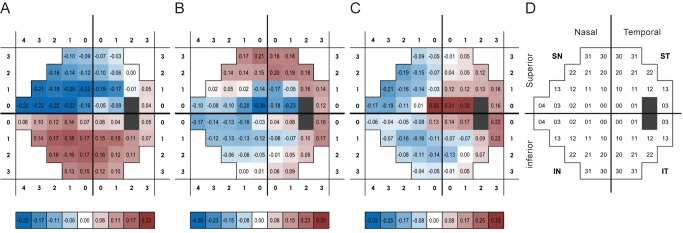
Fig. 4
Temporal loadings of three components. (A) Component 1 showed clear linear pattern. (B) Component 2 and (C) component 3 did not show the same trend (time 1 = initial follow-up, time 6 = last follow-up).
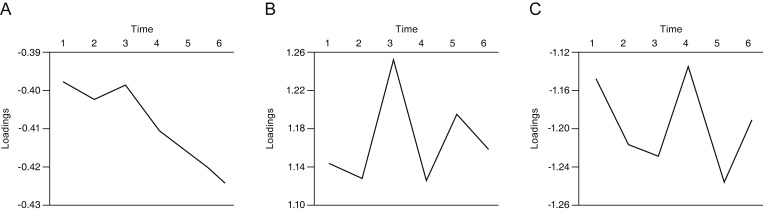
Fig. 5
Histogram of subject loadings by group. PG subjects had wider and subnormal distributions compared to PPG subjects in (A) component 1, (B) component 2, and (C) component 3. (A) Component 1 showed clear variability. PPG = pre-perimetric glaucoma; PG = perimetric glaucoma.
- TOOLS





 PDF Links
PDF Links PubReader
PubReader Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC Download Citation
Download Citation Print
Print