Over several decades, many different methods have been introduced to improve the accuracy of the intraocular lens (IOL) power calculation in eyes that have previously undergone myopic corneal refractive surgery [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. There are three primary reasons for unexpected IOL power calculation outcomes in these eyes. First, inaccurate measurement of anterior corneal curvature by standard keratometry can occur [
17]. Second, the standardized keratometric index of 1.3375 is no longer appropriate in these eyes because of changes in the anterior/posterior corneal curvature relationship after corneal refractive surgery [
17]. Lastly, third generation IOL calculation formulas (e.g., Hoffer Q, Holladay 1, SRK/T) erroneously predict effective lens position (ELP) [
17,
18,
19,
20]. The accuracy of the IOL power calculation formula depends on accurate corneal curvature measurement and ELP prediction.
Most studies have adjusted the keratometry value (K) for more accurate IOL power calculations. However, the Haigis-L, and the K-independent methods have been introduced as studies to estimate ELP accurately after corneal refractive surgery [
16,
21]. Postoperative ELP prediction accuracy is the major limiting factor in modern IOL power calculation accuracy [
15]. The SRK/T formula is best for eyes with a long axial length (AL) [
22]. SRK/T was developed using theoretical formulas as its foundation, but empirical regression methodology was used for optimization [
19]. Thus, preoperative actual measurement of the eyes may be correlated with estimation of ELP. Ho et al. [
21], showed a statistically significant correlation between theoretical corneal height (CH) and that measured with the Pentacam (Oculus Optikgerate GmbH, Wetzlar, Germany). Anterior segment optical coherence tomography (AS-OCT) is based on low coherence interferometry and provides a detailed two-dimensional, cross-sectional image of the anterior chamber [
23]. In eyes with a history of corneal refractive surgery, direct CH measurement with this high-resolution instrument may help to improve the accuracy of ELP estimates.
Herein, we introduce a novel method to predict relevant ELP and IOL power using CH measured with AS-OCT in eyes with a history of myopic corneal refractive surgery. To the best of our knowledge, this is the first time that CH measured with AS-OCT has been used in accurate IOL power calculation accuracy following corneal refractive surgery. More specifically, the feasibility of this method in accurately estimating ELP and calculating IOL power was investigated in eyes with a history of corneal refractive surgery.
Materials and Methods
The institutional review board (IRB) of Seoul National University Hospital approved the study protocol (IRB no. 1312-037-540); the protocol complied with the tenets of the Declaration of Helsinki. We retrospectively analyzed preoperative and postoperative data of patients who had undergone cataract surgery at Seoul National University Hospital between January 2012 and April 2013. Thirty eyes (23 patients) had undergone myopia-correcting corneal refractive surgery prior to uncomplicated phacoemulsification cataract surgery. The patients who had zonular disruption were excluded. The types of refractive surgery performed on these eyes were photorefractive keratectomy (PRK), laser in situ keratomileusis (LASIK), and laser subepithelial keratomileusis (LASEK). All cataract surgeries were performed by a single surgeon (MKK).
Preoperative evaluations included measurement of corneal radius, AL, and CH. Corneal radius was measured with an autokeratorefractometer (Nidek KR-8900; Topcon, Tokyo, Japan) and IOL Master (Carl-Zeiss Meditec, Dublin, CA, USA). The AL was measured with contact A-scan ultrasonography (Axis II PR; Quantel Medical, Clermont-Ferrand, France) and IOL Master. Topographic analysis with Orbscan IIz (Bausch & Lomb, Claremont, CA, USA) was also performed. CH was measured using Visante AS-OCT (Carl Zeiss Meditec). To measure CH, a line connecting the two anterior chamber angles was drawn in the AS-OCT image. A line was then drawn from the corneal vertex, perpendicular to the line connecting the anterior chamber angles. The distance between the posterior corneal surface and the intersection point of these two lines was defined as measured CH (CH
m) (
Fig. 1). The built-in software of the Visante AS-OCT automatically CH
m when the posterior corneal surface and the intersection point of the angle and the corneal vertex lines were specified. All AS-OCT examinations were performed by one examiner.
All surgeries were performed using the Infiniti Vision System (Alcon Laboratories, Fort Worth, TX, USA) with the same ultrasonic and fluidic settings. A 2.75 mm self-sealing clear corneal incision was made on the temporal or superior side of the eye, according to the steep corneal meridian. A routine phaco-chop technique was used to remove the cataract. There were no intraoperative complications, including posterior capsule rupture. Several different foldable, posterior chamber IOL were implanted and included the Alcon IQ SN60WF (A-constant 118.7), the Alcon SA60AT (A-constant 118.9), the Abbott Medical Optics (AMO) Tecnis ZCB00 (A-Constant 118.8), and the AMO AR40e (A-constant 118.4). The implanted IOL power and spherical equivalent 1 month after surgery were noted. The IOL power that would achieve emmetropia (Preal) was calculated using actual IOL power and postoperative spherical equivalent.
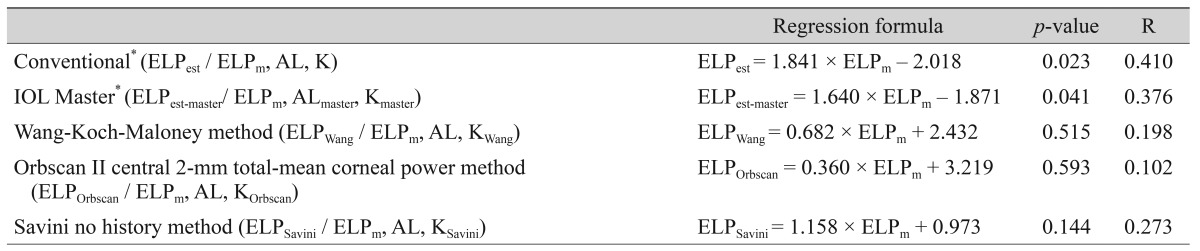
First, we investigated the best-fit regression formula to explain the relationship between estimated ELP (ELPest) and measured ELP (ELPm). We compared several linear regression formulas between ELPest and ELPm in various options, based on K or adjusted K, through the SRK/T formula. Thereafter, we selected the best-fit regression formula based on a high correlation coefficient (R) and statistical significance. Second, we evaluated the clinically relevant efficacy of the selected regression formula. Converted ELP (ELPconv) and IOL power (Pconv), obtained with the selected regression and SRK/T formulas, were compared with ELPest and Preal, respectively. In addition, mean error and mean absolute error between Pconv and Preal were examined. Finally, we compared the accuracy of our method with those previously documented and assessed method feasibility. Our calculations were performed with the following assumptions.
In the SRK/T formula [
19], the ELP-constant (ELP
const) was defined as the A-constant (A) of each IOL using the following formula:
ELPconst = 0.62467 ├Ś A - 68.747.
Offset for each IOL implanted was determined with the following equation: offset = ELPconst - 3.336.
The ELPm was calculated as follows: ELPm = CHm + offset.
Estimated postoperative ELP (ELP
est) was back-calculated using P
real, AL, and K, through the SRK/T formula. For back-calculations, we assumed that 1.00 diopter (D) of IOL prediction error produces 0.70 D of refractive error at the spectacle plane [
4,
16,
24]. The IOL Master was also used to back-calculate ELP
est-master from parameters K
master and AL
master. In addition, we evaluated the change of the ELP predicting accuracy in this method when we used adjusted K obtained by several IOL calculation methods after refractive surgery. After keratometric values were adjusted according to the Wang-Koch-Maloney method [
9], the Orbscan II central 2-mm total-mean corneal power method [
25], and the Savini no-history method [
14], each estimated ELP (ELP
Wang, ELP
Orbscan, ELP
Savini) value was back-calculated with P
real, AL, and each adjusted K (K
Wang, K
Orbscan, K
Savini) with the SRK/T formula. To investigate the relationship between estimated ELP obtained with various formulas using ELP
m, AL, and K, a stepwise linear regression was performed using IBM SPSS ver. 21.0 (IBM Corp., Armonk, NY, USA). This included ELP
est, (calculated with ELP
m, AL, and K), ELP
est-master (calculated with ELP
m, AL
master, and K
master), ELP
Wang (calculated with ELP
m, AL, and K
Wang), ELP
Orbscan (calculated with ELP
m, AL, and K
Orbscan), and ELP
Savini (calculated with ELP
m AL, and K
Savini), as shown in
Table 1 [
9,
14,
26]. Of these, the best-fit formula was selected for IOL power prediction. The following selected regression formula was used:
ELPest = 1.841 ├Ś ELPm - 2.018 (
p = 0.023, R = 0.410).
During computerized stepwise regression analysis, AL and K were dropped because they were not meaningful variables in this regression formula.
The ELPconv values were obtained by applying ELPm to this selected regression formula. Additionally, Pconv was calculated from ELPconv, AL, and K with the SRK/T formula. Agreement between ELPconv and ELPest and between Pconv and Preal is represented by Bland-Altman plots and expressed in terms of mean bias ┬▒1.96 standard deviations (SD). The difference between Pconv and Preal was defined as the mean error; the absolute value of mean error was defined as the mean absolute error. The proportion of eyes within ┬▒0.5, ┬▒1.0, ┬▒1.5, and ┬▒2.0 D of the predicted refractive error was investigated when Pconv was applied. Four additional methods were used to calculate IOL power for the comparison: 1) Orbscan II central 2-mm total-mean corneal power method + double-K method and the SRK/T formula; 2) Orbscan II central 2-mm total-mean corneal power method + double-K method and the Hoffer Q formula; 3) Shammas no-history method + double-K method and the SRK/T formula; 4) Savini no-history method + double-K method and the SRK/T formula. Preoperative corneal power used in the double-K method was substituted with 43.5 D, a value close to the mean of the study population.
All data were analyzed using IBM SPSS ver. 21.0. As described earlier, linear regression formulas were calculated and correlation coefficients were documented. Statistical significance was defined as p < 0.05.
Results
Thirty eyes from 23 patients were retrospectively analyzed.
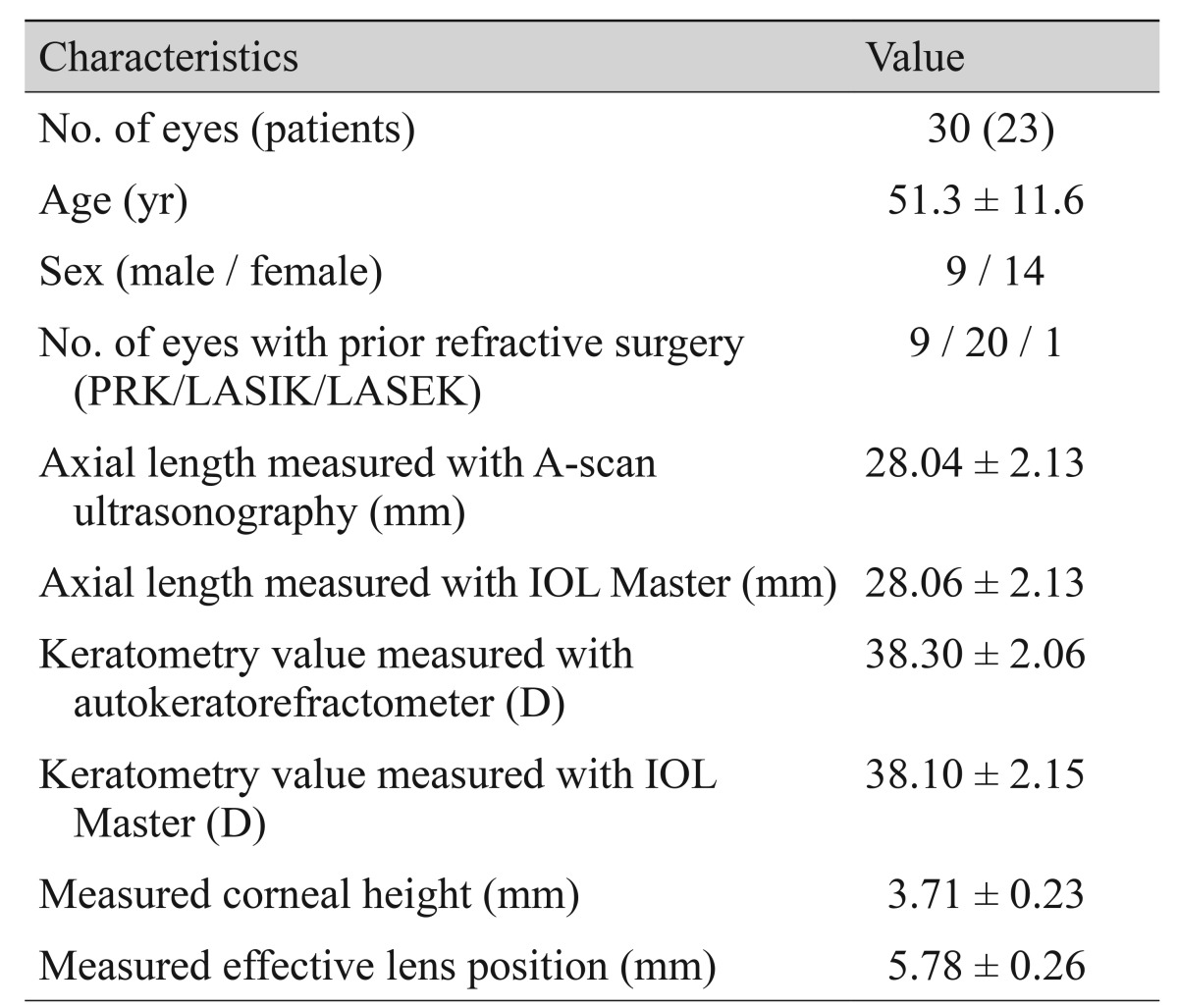
Table 2 summarizes patient demographic data. Mean age was 51.3 ┬▒ 11.6 years and mean AL, as measured using an A-scan, was 28.04 ┬▒ 2.13 mm. Mean keratometry value, obtained with an autokeratorefractometer, was 38.30 ┬▒ 2.06 D. The mean CH, ELP
est, and ELP
m were 3.71 ┬▒ 0.23, 7.74 ┬▒ 1.09, and 5.78 ┬▒ 0.26 mm, respectively. The number of eyes that had undergone PRK, LASIK, and LASEK were 9, 20, and 1, respectively. Four different IOL types were implanted, including the Alcon IQ SN60WF (n = 18 eyes), the Alcon Acrysof 1 piece SA60AT (n = 1 eye), the AMO Tecnis ZCB00 (n = 9 eyes), and the AMO Sensar AR40e (n = 2 eyes). Mean ELP
est was 7.74 ┬▒ 1.09 mm and the best linear regression formula (
Fig. 2) was, ELP
est = 1.841 ├Ś ELP
m - 2.018.
Mean ELP
conv was 7.74 ┬▒ 0.43 mm. Agreement between ELP
m and ELP
est is displayed in
Fig. 3. The difference between ELP
m and ELP
est was -0.0021 ┬▒ 1.00 mm (mean ┬▒ 1.96 SD; range, -1.97 to 1.62 mm). Agreement between P
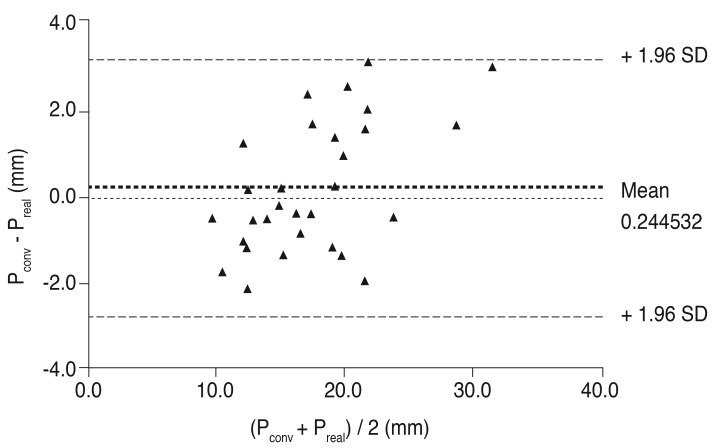
conv and P
real is displayed in
Fig. 4. The difference between P
conv and P
real was 0.90 ┬▒ 1.24 D (mean ┬▒ 1.96 SD; range, -1.14 to 3.17 D) (
Fig. 4). The mean absolute error was 1.27 ┬▒ 0.83 D (range, 0.03 to 3.17 D).
Figs. 3 and
4 show considerable agreement between ELP
m and ELP
est, and P
conv and P
real, respectively. The percentages of eyes within ┬▒0.5, ┬▒1.0, ┬▒1.5, and ┬▒2.0 D of the refractive error were 23.3%, 66.6%, 83.3%, and 100.0%, respectively (
Table 3) [
4,
16,
25]. These percentages were compared to those calculated with the four additional methods and in another study [
25] (
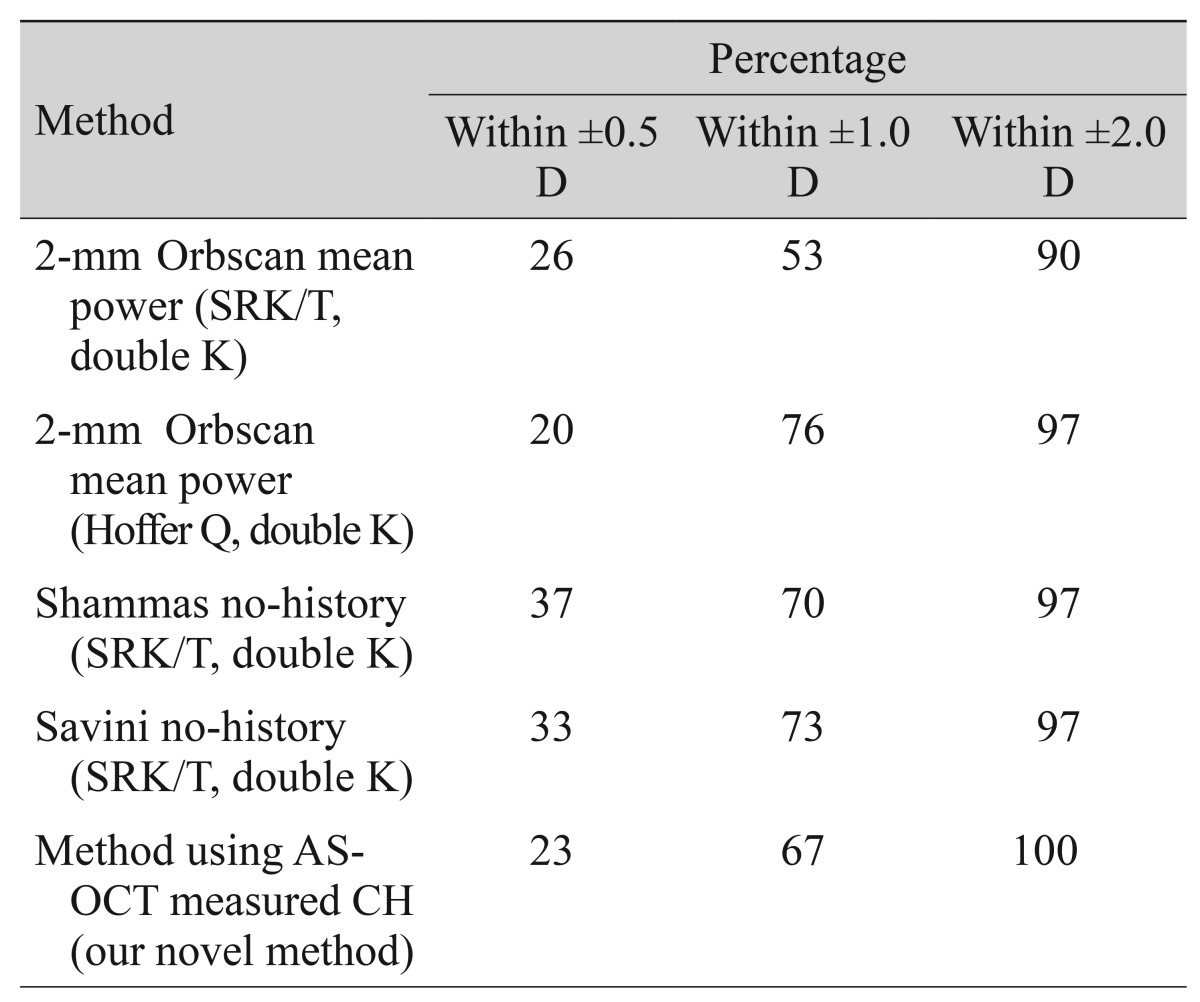
Table 4). We found that our method provided relatively similar results compared to others.
Discussion
Our study described ELP estimation and IOL power calculation methods using CH measured with AS-OCT. Our method showed tolerable IOL power prediction in the SRK/T formula and confirmed that measured ELP was closely correlated with theoretical ELP.
The CH is important in ELP prediction with the Holladay and SRK/T formulas [
26], but this CH is a theoretical value calculated from K and AL. It is known that theoretical CH is meaningful in ELP estimation, not actual CH. Ho et al. [
21] showed that CH measured with Pentacam is well-correlated with theoretical CH (R = 0.91,
p < 0.001). It is known that actual CH is closely related to anterior chamber depth (ACD) [
27] and that ELP is significantly correlated with ACD [
28]. Therefore, actual CH can be also related to ELP.
IOL power calculation in eyes that have undergone corneal refractive surgery is challenging for many reasons. When the K value after refractive surgery is directly applied, an incorrect ELP estimation can occur with third or fourth generation formulas, leading to erroneous IOL power predictions. Previous studies related with IOL power calculations after refractive surgery focused on effective corneal power measurements or relevant conversions. Olsen [
15] showed that ELP prediction errors are the major determinants of IOL power prediction errors. To solve this problem, the double-K method has been widely used and has improved IOL power prediction accuracy. In this method, the K value measured before refractive surgery is used for ELP estimation. Nishimura et al. [
29] showed that central ACD significantly decreases after LASIK in younger patients (<40 years), but not in older patients. The majority of corneal refractive surgery patients are in their twenties or thirties. Thereafter, the CH can decrease with age. Therefore, ELP estimation using preoperative K values in the double-K method may induce errors due to age-related decreases in ACD, and CH would not be reflected accurately. Direct measurement of parameters related to ELP can improve ELP estimation accuracy. Based on these deductions, we developed an ELP estimation method that utilizes measured CH. The Haigis-L formula utilizes ACD measurement and subtracts 0.35 D from the effective equivalent corneal power to help calculate relevant IOL power [
16]. Unfortunately, the Haigis-L formula is proprietary and cannot be accessed, so its further development is not possible.
Both the AS-OCT and Pentacam provide good anterior segment images and have high intraobserver reliability and good inter-method agreement for ACD measurements [
30,
31]. The CH measured with either the AS-OCT or the Pentacam is also relatively accurate. When applying our method to ELP predictions, both AS-OCT and Pentacam are thought to provide suitable direct measurement of CH.
When our method was applied, the proportion of eyes within ┬▒1.0, ┬▒1.5, and ┬▒2.0 D of the refractive error was 66.6%, 83.3%, and 100.0% respectively. Additionally, P
conv and ELP
conv showed good agreement with P
real and ELP
est, respectively. In comparing the accuracy of IOL power calculation for eyes with a history of myopic refractive surgery, our methods showed comparable accuracy with other conventional methods (
Table 4). We chose the Shammas no-history, Savini no-history, and Orbscan II central 2-mm total-mean corneal power methods for K value modification because they have been relatively accurate in our clinical experience. McCarthy et al. [
32] and Arce et al. [
25] reported that 80.9% and 97.7% of eyes and 77% and 96% of eyes were within ┬▒1.0 and ┬▒2.0 D, respectively. However, our study did not show results as good as the two reports above. The accuracy of each IOL calculation method seemed to depend on several surgical factors. Most IOL calculation formulas [
18,
19,
20], including the SRK/T formula, assume that the cornea is perfectly spherical and converting corneal radius to diopters is performed using a keratometric refractive index of 1.3375 [
3,
5,
33]. However, most other K-adjusting methods utilize other theoretical indices to correct this keratometric refractive index [
33]. Therefore, regression formulas in which adjusted K values are applied may not be suitable models to use with the SRK/T formula. The AL and K values were not considered in our formula, thus relevant corneal power was not considered in IOL power calculations. The application of effective corneal power is quite important in IOL power calculations after refractive surgery. Nevertheless, relatively good predictive outcomes were obtained with our method when only converted ELP values were applied. Our results imply that relevant ELP estimation may be quite important, as much as AL and K, in IOL power calculations for eyes that had previously undergone corneal refractive surgery.
There are several limitations in this study. A limited sample size and retrospective study were used for obtaining the IOL power prediction formula and analyzing refractive prediction error. As discussed above, AL and K were not considered in the regression formula. Additionally, the surgeon factor and the adjustment for different types of IOL and intraobserver variability were not considered. Our method is not yet ready for clinical application, but our findings may help to improve ELP estimation accuracy for IOL power calculations. Recently, the Fourier-domain OCT-based IOL power calculation method was introduced and showed good predictive accuracy in patients with a history of myopic laser vision correction [
34]. With this method, the posterior corneal power can be accurately measured with Fourier-domain OCT. If an accurate corneal power measurement and relevant ELP estimation using AS-OCT is performed and applied, a more satisfactory IOL power prediction formula can be developed.
In conclusion, an IOL power calculation using CH may be helpful in patients who need cataract surgery and have undergone prior corneal refractive surgery. Further study, including a larger sample size, is needed to improve the accuracy of our IOL power calculation method.
Notes
This study was presented in the 110th Conference of Korean Ophthalmologic Society, 2013.
Conflicts of interest
Conflict of Interest: No potential conflict of interest relevant to this article was reported.
REFERENCES
1. Holladay JT. Consultations in refractive surgery.
Refract Corneal Surg 1989;5:202-203.


2. Hoffer KJ. Intraocular lens power calculation for eyes after refractive keratotomy.
J Refract Surg 1995;11:490-493.


3. Seitz B, Langenbucher A. Intraocular lens power calculation in eyes after corneal refractive surgery.
J Refract Surg 2000;16:349-361.


4. Feiz V, Mannis MJ, Garcia-Ferrer F, et al. Intraocular lens power calculation after laser in situ keratomileusis for myopia and hyperopia: a standardized approach.
Cornea 2001;20:792-797.


5. Speicher L. Intra-ocular lens calculation status after corneal refractive surgery.
Curr Opin Ophthalmol 2001;12:17-29.


6. Rosa N, Capasso L, Romano A. A new method of calculating intraocular lens power after photorefractive keratectomy.
J Refract Surg 2002;18:720-724.


7. Haigis W. Corneal power after refractive surgery for myopia: contact lens method.
J Cataract Refract Surg 2003;29:1397-1411.


8. Ferrara G, Cennamo G, Marotta G, Loffredo E. New formula to calculate corneal power after refractive surgery.
J Refract Surg 2004;20:465-471.


9. Wang L, Booth MA, Koch DD. Comparison of intraocular lens power calculation methods in eyes that have undergone LASIK.
Ophthalmology 2004;111:1825-1831.


10. Latkany RA, Chokshi AR, Speaker MG, et al. Intraocular lens calculations after refractive surgery.
J Cataract Refract Surg 2005;31:562-570.


11. Camellin M, Calossi A. A new formula for intraocular lens power calculation after refractive corneal surgery.
J Refract Surg 2006;22:187-199.


12. Jarade EF, Abi Nader FC, Tabbara KF. Intraocular lens power calculation following LASIK: determination of the new effective index of refraction.
J Refract Surg 2006;22:75-80.


13. Masket S, Masket SE. Simple regression formula for intraocular lens power adjustment in eyes requiring cataract surgery after excimer laser photoablation.
J Cataract Refract Surg 2006;32:430-434.


14. Savini G, Barboni P, Zanini M. Intraocular lens power calculation after myopic refractive surgery: theoretical comparison of different methods.
Ophthalmology 2006;113:1271-1282.


15. Olsen T. Calculation of intraocular lens power: a review.
Acta Ophthalmol Scand 2007;85:472-485.


16. Haigis W. Intraocular lens calculation after refractive surgery for myopia: Haigis-L formula.
J Cataract Refract Surg 2008;34:1658-1663.


17. Saiki M, Negishi K, Kato N, et al. A new central-peripheral corneal curvature method for intraocular lens power calculation after excimer laser refractive surgery.
Acta Ophthalmol 2013;91:e133-e139.


18. Holladay JT, Prager TC, Chandler TY, et al. A three-part system for refining intraocular lens power calculations.
J Cataract Refract Surg 1988;14:17-24.


19. Retzlaff JA, Sanders DR, Kraff MC. Development of the SRK/T intraocular lens implant power calculation formula.
J Cataract Refract Surg 1990;16:333-340.


20. Hoffer KJ. The Hoffer Q formula: a comparison of theoretic and regression formulas.
J Cataract Refract Surg 1993;19:700-712.


21. Ho JD, Liou SW, Tsai RJ, Tsai CY. Estimation of the effective lens position using a rotating Scheimpflug camera.
J Cataract Refract Surg 2008;34:2119-2127.


22. Aristodemou P, Knox Cartwright NE, Sparrow JM, Johnston RL. Formula choice: Hoffer Q, Holladay 1, or SRK/T and refractive outcomes in 8108 eyes after cataract surgery with biometry by partial coherence interferometry.
J Cataract Refract Surg 2011;37:63-71.


23. Doors M, Berendschot TT, de Brabander J, et al. Value of optical coherence tomography for anterior segment surgery.
J Cataract Refract Surg 2010;36:1213-1229.


24. Yang R, Yeh A, George MR, et al. Comparison of intraocular lens power calculation methods after myopic laser refractive surgery without previous refractive surgery data.
J Cataract Refract Surg 2013;39:1327-1335.


25. Arce CG, Soriano ES, Weisenthal RW, et al. Calculation of intraocular lens power using Orbscan II quantitative area topography after corneal refractive surgery.
J Refract Surg 2009;25:1061-1074.


26. Olsen T, Corydon L, Gimbel H. Intraocular lens power calculation with an improved anterior chamber depth prediction algorithm.
J Cataract Refract Surg 1995;21:313-319.


27. Tomlinson A, Leighton DA. Ocular dimensions in the heredity of angle-closure glaucoma.
Br J Ophthalmol 1973;57:475-486.



28. Olsen T. Prediction of the effective postoperative (intraocular lens) anterior chamber depth.
J Cataract Refract Surg 2006;32:419-424.


29. Nishimura R, Negishi K, Dogru M, et al. Effect of age on changes in anterior chamber depth and volume after laser in situ keratomileusis.
J Cataract Refract Surg 2009;35:1868-1872.


30. Doors M, Cruysberg LP, Berendschot TT, et al. Comparison of central corneal thickness and anterior chamber depth measurements using three imaging technologies in normal eyes and after phakic intraocular lens implantation.
Graefes Arch Clin Exp Ophthalmol 2009;247:1139-1146.



31. Yi JH, Hong S, Seong GJ, et al. Anterior chamber measurements by pentacam and AS-OCT in eyes with normal open angles.
Korean J Ophthalmol 2008;22:242-245.



32. McCarthy M, Gavanski GM, Paton KE, Holland SP. Intraocular lens power calculations after myopic laser refractive surgery: a comparison of methods in 173 eyes.
Ophthalmology 2011;118:940-944.


33. Sonego-Krone S, Lopez-Moreno G, Beaujon-Balbi OV, et al. A direct method to measure the power of the central cornea after myopic laser in situ keratomileusis.
Arch Ophthalmol 2004;122:159-166.


34. Tang M, Wang L, Koch DD, et al. Intraocular lens power calculation after previous myopic laser vision correction based on corneal power measured by Fourier-domain optical coherence tomography.
J Cataract Refract Surg 2012;38:589-594.



Fig.┬Ā1
An anterior segment optical coherence tomography image. The measured corneal height (CHm) was defined as the distance between the posterior corneal surface and the intersection between the perpendicular lines.
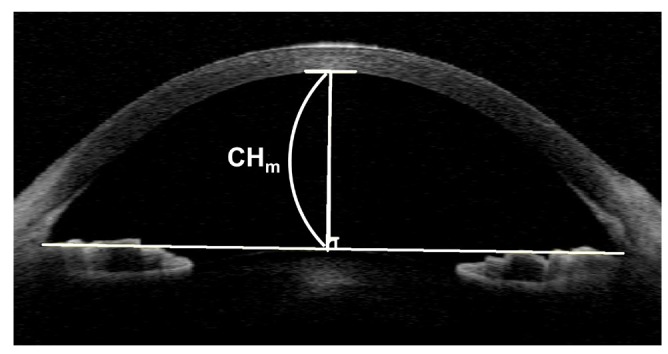
Fig.┬Ā2
Linear regression analysis of measured effective lens position (ELPm) and the estimated effective lens position (ELPest).
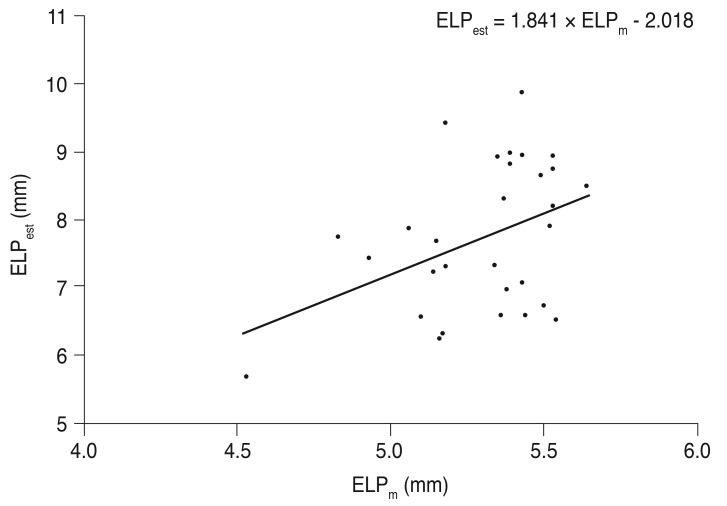
Fig.┬Ā3
Bland-Altman plot showing differences between measured
effective lens position (ELPm) and estimated effective lens position (ELPest). Lines showing the mean difference and the ┬▒1.96 standard deviation (SD) limits are also shown.
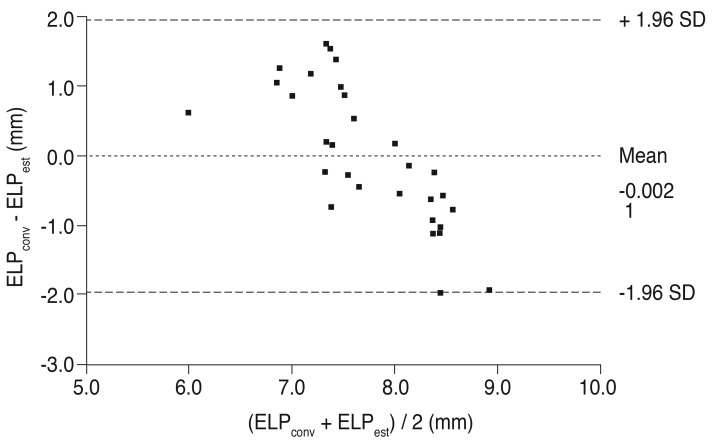
Fig.┬Ā4
Bland-Altman plot showing differences between the converted intraocular lens power (Pconv) and the actual intraocular lens power (Preal). Lines showing the mean difference and the ┬▒1.96 standard deviation (SD) limits are also shown.
Table┬Ā1
Various stepwise linear regression formulas examined
Table┬Ā2
Summary of patient demographic data
Table┬Ā3
ME, MAE, and percentages of eyes within a refractive prediction error when the Pconv was used*

Table┬Ā4
Percentage of eyes within a refractive prediction error using various intraocular lens calculation methods













 PDF Links
PDF Links PubReader
PubReader Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC Download Citation
Download Citation Print
Print